
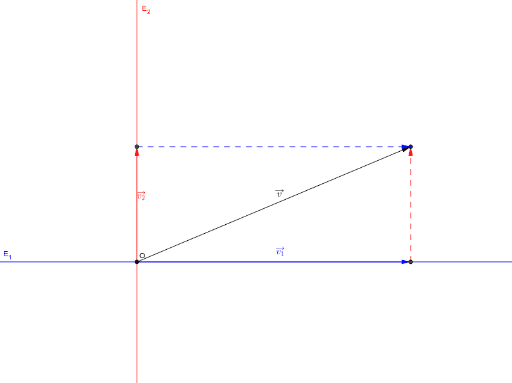
Here, we are optimizing a quadratic equation with linear constraint. Maximizing is same as minimizing the that is, we need to find w and b such that: We need to maximize the geometric margin such that: Or, the above equation for each data point: The distance equation for a data point to hyperplane for all items in the data could be written as: Now, solving for r gives following equation: Replace x’ by x in the linear classifier equation gives: A unitary vector in the direction of this normal vector is given by. The shortest distance b/w them is of course the perpendicular distance i.e parallel to the normal vector. However, the functional margin is by definition of above is unconstraint, so we need to formulize the distance b/w a data point x and the decision boundary. The value of class label here can be only either be -1 or +1 (for 2-class problem). Now, consider the training D such that where represents the n-dimesnsional data point and class label respectively. Now since all the plane x in the hyperplane should satisfy the following equation: Here b is used to select the hyperplane i.e perpendicular to the normal vector. These are commonly referred to as the weight vector in machine learning. Below is the method to calculate linearly separable hyperplane.Ī separating hyperplane can be defined by two terms: an intercept term called b and a decision hyperplane normal vector called w. Generally, the margin can be taken as 2* p, where p is the distance b/w separating hyperplane and nearest support vector. Thus, the best hyperplane will be whose margin is the maximum. This distance b/w separating hyperplanes and support vector known as margin. The idea behind that this hyperplane should farthest from the support vectors. Now, we understand the hyperplane, we also need to find the most optimized hyperplane. So, why it is called a hyperplane, because in 2-dimension, it’s a line but for 1-dimension it can be a point, for 3-dimension it is a plane, and for 3 or more dimensions it is a hyperplane Such a line is called separating hyperplane. In the above scatter, Can we find a line that can separate two categories. The optimal hyperplane comes from the function class with the lowest capacity i.e minimum number of independent features/parameters. Support vectors are the data points that are close to the decision boundary, they are the data points most difficult to classify, they hold the key for SVM to be optimal decision surface.
I know the matrix representation of a regression can be quite confusing at the beginning but eventually it simplifies a lot when deriving more complex algebra. However, I have already devised the solution here and I stand corrected if I am wrong on that one.) ( Edit: I just realized that for your second question this is exactly the opposite of you have written regading inclusion or exclusion of the constant.
#HYPERPLAN VECTORIEL EQUATION FULL#
Since $X$ has full rank per definition, $y-X\beta=0$, and so the regression passes through the origin if we leave out the intercept. This generalizes to multiple dimensions, as it will be seen later for when deriving $\beta$: If we leave out the constant, the regression hyperplane always passes trivially through $$ - no doubt. It can be further shown that it also passes through $$ for when the constant is included. I am reading Elements of Statistical Learning and on page 12 (section 2.3) a linear model is notated as:


 0 kommentar(er)
0 kommentar(er)
